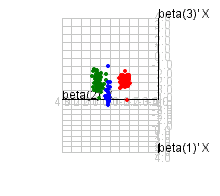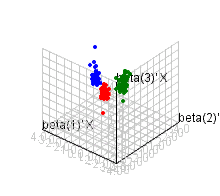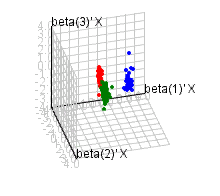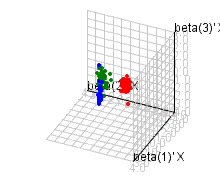
Abstract
Sliced inverse regression (SIR) was introduced by Li
(1991) to find the effective dimension reduction directions for
exploring the intrinsic structure of high-dimensional data. In this
study, we propose a hybrid SIR method using a kernel machine which we
call kernel SIR. The kernel mixtures result in the transformed data
distribution being more Gaussian like and symmetric; providing more
suitable conditions for performing SIR analysis. The proposed method can
be regarded as a nonlinear extension of the SIR algorithm. We provide a
theoretical description of the kernel SIR algorithm within the framework
of reproducing kernel Hilbert space (RKHS). We also illustrate that
kernel SIR performs better than several standard methods for
discriminative, visualization, and regression purposes. We show how the
features found with kernel SIR can be used for classification of
microarray data and several other classification problems and compare
the results with those obtained with several existing dimension
reduction techniques. The results show that kernel SIR is a powerful
nonlinear feature extractor for classification problems.
Keywords: Dimension reduction;
Kernel machines; Reproducing kernel Hilbert space; Visualization.
[Full Text]
ˇ@ |
Supplemental Material
Examples for Visualization Using PCA, SIR, KPCA, and KSIR
*DesU: Description from
UCI machine
learning repository.
Examples for Exploring Global Structure Using SIR and KSIR
*RegD: the data is obtained and
pre-processed in Regression DataSets by Dr. Luís
Torgo
http://www.liacc.up.pt/~ltorgo/Regression/DataSets.html
*The first column in the data file
(*.txt) is the response variable.
*Exploration of global structure using SIR and KSIR is useful for regression
problems.
Program/Routine/R-package
- jDRCluster:
java-designed software for dimension reduction, cluster analysis and exploratory data analysis
(under development).
-
dr: Methods for dimension reduction for regression (R package).
-
kernlab: Kernel Methods Lab (R package).
- e1071
(svm): Misc Functions of the Department of Statistics (e1071), TU Wien (R
package).
Useful Links
ˇ@ |
Main Reference
-
Huang, S. Y., Hwang, C. R., and Lin, M. H.
(2005), ˇ§Kernel Fisher Discriminant Analysis
in Gaussian Reproducing Kernel Hilbert Space,ˇ¨ Manuscript.
http://www.stat.sinica.edu.tw/syhuang.
-
Lee, Y. J., and Huang, S. Y. (2006), ˇ§Reduced
Support Vector Machines: a Statistical
Theory,ˇ¨ IEEE Transactions on Neural Networks, to appear.
http://dmlab1.csie.ntust.edu.tw/downloads.
-
Li, K. C. (1991), ˇ§Sliced Inverse Regression
For Dimension Reduction,ˇ¨ Journal of The American Statistical Association,
86, 316 ˇV 342.
-
Murphy, P. M., and Aha, D. W. (1993), UCI
Repository of Machine Learning Databases.
University of California, Department of Information and Computer Science,
Irvine, CA.
-
Sch¨olkopf, B., and Smola, A. J. (eds.)
(2002), Learning With Kernels: Support Vector
Machines, Regularization, Optimization, and Beyond, MIT Press, Cambridge,
MA.
Sch¨olkopf, B., Smola, A., and M¨uller, K. R. (1998), ˇ§Nonlinear Component
Analysis as
a Kernel Eigenvalue Problem,ˇ¨ Neural Computation, 10, 1299 ˇV 1319.
-
Sch¨olkopf, B., Tsuda, K., and Vert, J.-P.
(eds.) (2004), Kernel Methods in Computational Biology, MIT Press.
|
|